Una breve dimostrazione sull’uso del Kriging Ordinario per dati batimetrici in R
Caricamento delle librerie necessario
Il kriging ordinario è una tecnica statistica per l’interpolazione dei dati. carico le le librerie necessarie allo svolgimento dell’esercizio ed in particolare rgdal permette di importare ed esportare in R i layer geografici. La libreria gstat è quella che ha implementato tutte le funzioni geostatistiche.
library(rgdal)
## Loading required package: sp
## rgdal: version: 1.4-4, (SVN revision 833)
## Geospatial Data Abstraction Library extensions to R successfully loaded
## Loaded GDAL runtime: GDAL 2.2.3, released 2017/11/20
## Path to GDAL shared files: /usr/share/gdal/2.2
## GDAL binary built with GEOS: TRUE
## Loaded PROJ.4 runtime: Rel. 4.9.3, 15 August 2016, [PJ_VERSION: 493]
## Path to PROJ.4 shared files: (autodetected)
## Linking to sp version: 1.3-1
library(gstat)I dati
Nell’esempio che segue utilizzerò uno shape di punti di una batimetria del Lago di Montedoglio (lago artificiale) nella cui tabella attributi è presente un campo quota che riporta i livelli di quota del fondo misurato in una campagna del 2010. Lo scopo è quello di interpolare tali livelli di falda con il kriging ordinario.

Qualora voleste rifare l’esercizio autonomamente, per avere il link del dato è richiesta la compilazione del form qui sotto.
importo i dati
batim = readOGR(dsn="~/Dropbox/kriging-intro/", layer="punti")OGR data source with driver: ESRI Shapefile
Source: "/home/pierluigi/Dropbox/kriging-intro", layer: "punti"
with 16160 features
It has 3 fieldssummary(batim)Object of class SpatialPointsDataFrame
Coordinates:
min max
coords.x1 260002 265407
coords.x2 4830323 4835842
Is projected: TRUE
proj4string :
[+proj=utm +zone=33 +ellps=intl +units=m +no_defs]
Number of points: 16160
Data attributes:
dbl_1 dbl_2 quota
Min. :260002 Min. :4830323 Min. :346.8
1st Qu.:262284 1st Qu.:4831236 1st Qu.:362.2
Median :263240 Median :4831855 Median :374.7
Mean :263006 Mean :4832184 Mean :371.9
3rd Qu.:263770 3rd Qu.:4832603 3rd Qu.:383.4
Max. :265407 Max. :4835842 Max. :387.2Analisi statistica dei dati di batimetria del 2010
La necessità di questa analisi è verificare il comportamento statistico del dataset, verificare ad esempio se esistono valori di outlier (legati ad esempio un qualche errore grossolano che potrebbe essere stato commesso) o verificare se i dati appartengono ad una stessa popolazione o meno. quota indica il nome della colonna che contiene i dati della batimetria.Hide
hist(batim$quota,nclass=20,col="lightblue",main="Istogramma")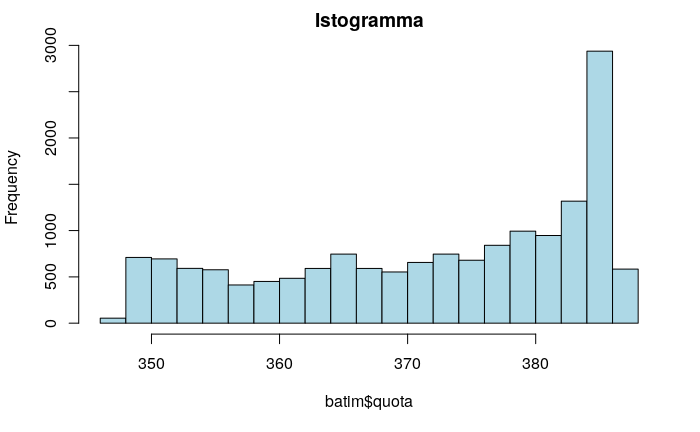
# plotta l'istogramma dei dati della quota del 2010 dividendo il range in 20 classi,
#quota indica il nome della colonna che contiene i dati di livello
plot(density(batim$quota),main="Mappa di densità")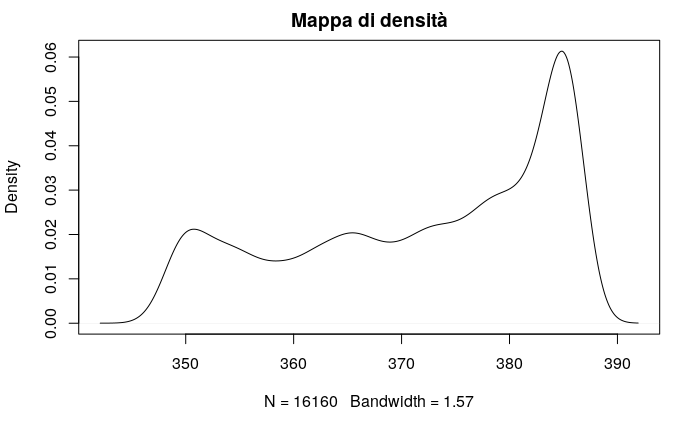
# plotta la curva densità di frequenza della quota 2010, secondo un kernel gaussianoQuesti due grafici dicono che il dataset presenta una sola popolazione, poiché presenta un unico massimo, si può quindi affermare quasi con certezza che i dati si riferisco ad un’unica falda. Osservato che esiste un’unica popolazione andiamo a verificare la presenza di eventuali outliers, cioè quei valori molto lontano dalla media che ricadono (tipicamente) prima del 5° percentile o dopo 95° percentile, tramite la costruzione del boxplot del dataset.Hide
boxplot(batim$quota)

Dal boxplot si può vedere che non esistono outlier nel nostro set di dati in quanto non si ha nessun punto che sta oltre il 5° (linea orizzontale più in basso) o il 95° (linea orizzontale più in alto) percentile e che la media dei valori è a circa 300 metri.
Geostatistica – kriging ordinario
Variogramma sperimentale
la prima fase di uno studio geostatistico è studiare il lvariogramma dei dati. Si deve plottareil variogramma del livello della batimetria del 2010, QUOTA.
plot(variogram(quota~1,loc=batim,cutoff=2500,width=100))
Il termine ~1 indica il kriging ordinario (cioè si assume il dato grezzo senza eseguire una detrendizzazione), loc localizza i dati da trattare, cutoff è la distanza massima entro la quale si prendono i dati da interpolare, width è il passo con qui vengono presi i dati (lag). Dal variogramma si vede chiaramente che la serie di dati presenta un comportamento della varianza classica dove a brevi distanze i dati sono più correlati che a grandi distanze. Ovvero coppie di punti quotati sono più simili se si trovano ad una distanza piccola rispetto a coppie di punti che si trovano ad una distanza più grande. Questo comportamento è ovvio ma lo possiamo visualizzare proprio attraverso questo grafico del variogramma sperimentale.
modello del variogramma
Il passaggio successivo consiste nel modellare il variogramma sperimentale con un modello numerico di variogramma. In base all’andamento generale del variogramma i modelli che intuitivamente meglio lo possono approssimare sono quello sferico o quello esponenziale. Il modello che deve essere scelto è quello che fornisce gli errori più contenuti nel processo di cross validation del kriging. Individueremo dapprima il modello di variogramma “a occhio” e poi attraverso la procedura di fitting. In basi ai valori ottenuti si sceglierà il modello migliore.
#salvo ilmodello
mod_vgm=vgm(model="Sph",psill=160,nugget=4,range=1500)
#visualizzo il modello
plot(variogram(quota~1,loc=batim,cutoff=2500,width=100),mod_vgm)
il comando vgm(), “Sph” indica il modello sferico, che viene definito tramite psill, nugget e range.
Variogramma “fittato”
Il passaggio successivo è quello di calcolare un variogramma fittato sulla base dei dati.
vgm_fit=fit.variogram(variogram(quota~1,loc=batim,cutoff=2500,width=100),mod_vgm)
plot(variogram(quota~1,loc=batim,cutoff=2500,width=100),vgm_fit)
La validazione dei modelli
La validazione dei modelli, effettuata tramite la cross validation, è una parte molto importante del lavoro in quanto permettedi determinare quale sia il modello di variogramma migliore per il nostro set di dati. In questo caso dobbiamo scegliere tra il modello “a occhio” e quello fittato.
La cross validation si esegue in R tramite il comando krige.cv.
#cv per il modello a occhio
mod_vgm.cv=krige.cv(quota~1,loc=batim,model=mod_vgm,nfold=5,maxdist=100,verbose=T)
#cv per il modello fittato
mod_vgm_fit.cv=krige.cv(quota~1,loc=batim,model=vgm_fit,nfold=5,nmax=100,verbose=T)nfold=5 indica che i dati vengono divisi in 5 gruppi ed alternativamente si toglie un gruppo alla volta. Ho inserito il parametro maxdist per utilizzare la massimo i punti nell’intorno di 100 metri per non chiedere troppe risorse di calcolo.
Sommari statistici
#sommari
summary(mod_vgm.cv$residual)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## -7.8670 -0.2773 0.0058 -0.0099 0.2705 13.1923 571
summary(mod_vgm_fit.cv$residual)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## -6.9869 -0.3645 -0.0021 -0.0158 0.3430 12.4198 615
#Istogrammi
hist(mod_vgm.cv$residual,nclass=20,xlim=range(-15,15),col="lightblue",main="Istogramma dei residui")
hist(mod_vgm_fit.cv$residual,nclass=20,xlim=range(-15,15),col="lightblue",main="Istogramma dei residui fittato")
#RMSE
sqrt(mean(mod_vgm.cv$residual^2,na.rm=T))
## [1] 0.7045771
sqrt(mean(mod_vgm_fit.cv$residual^2,na.rm = T))
## [1] 0.8566958Dai risultati possiamo vedere che il modello che presenta la maggiore accuratezza, cioè con media dei residui più vicina a zero sia mod_vgm_fit quello fittato. La precisione invece determinata dall’errore minimo quadrato (RMSE), quindi il modello più preciso quello che presenta RMSE più basso (0.64 contro 0.76 del modello mod_vgm) è sempre mod_vgm_fit.
Interpolazione con Kriging Ordinario – Ordinary Kriging
Dopo aver accuratamente analizzato i risultati della cross validation e scelto il modello più appropriato, si passa alla costruzione della griglia su cui interpolare.
grd =makegrid(batim,"regular", cellsize = c(20,20))
coordinates(grd) <- c("x1", "x2")
gridded(grd) <- TRUE # Create SpatialPixel object
fullgrid(grd) <- TRUE # Create SpatialGrid object
#assegna il CRS dalla abtimetria
proj4string(grd)<-proj4string(batim)Interpolamo i dati:
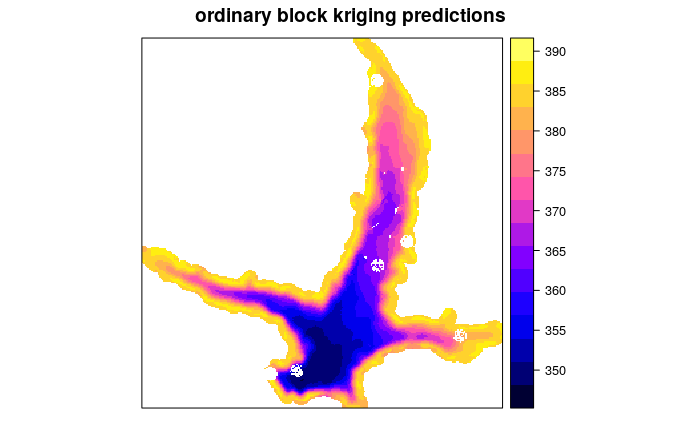
La particolarità di questa operazione è aver utilizzato il kriging a blocchi quadrati di 100 metri in modo da mediare meglio la densità dei dati che non è spazialmente distribuita. Inoltre il parametro maxdist pari a 100 non utilizza punti più lontani di 100 metri per fare l’interpolazione (solo i più vicini vengono usati nel calcolo). Infatti la mappa finale ha i bianchi nelle aree più lontane dai punti.
batim.ok=krige(quota~1,loc=batim,model=mod_vgm,newdata=grd,nmax=100,block=c(100,100))
spplot(batim.ok["var1.pred"], main = "ordinary block kriging predictions")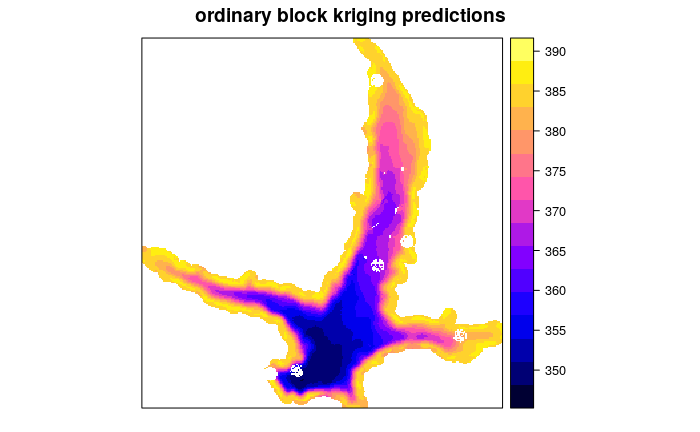
Ulteriore aspetto da visualizzare è la mappa delle varianze
spplot(batim.ok["var1.var"], main = "ordinary block kriging variance")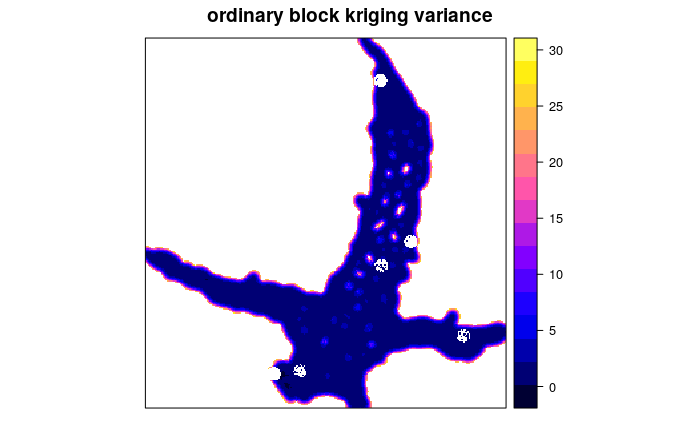
Sitografia
- Corso di geostatistica: http://www.css.cornell.edu/faculty/dgr2/teach/degeostats.html
Per approfondimenti
- Prova i nostri corsi. Abbiamo disponibile anche un corso di geostatistica ed un corso di QGIS base.

Lascia un commento
Devi essere connesso per inviare un commento.