La regressione geografica ponderata come metodo per comprendere se due elementi hanno una dipendenza di tipo spaziale
In questo tutorial voglio introdurre una tecnica statistica che si applica a dati spaziali denominata Regressione Geografica Pesata o GWR. Per chiarivi partiamo da un esempio pratico.
Supponiamo di avere i dati di vendita di abitazioni del 2001 di alcuni quartieri di Londra. Per ogni vendita abbiamo diverse informazioni come ovviamente il prezzo di vendita, metratura dell’abitazione, numero di piani, tasso di occupazione delle persona che vi abitano nei settori professionali/manageriali. In genere è logico aspettarsi che il prezzo medio al metro quadro dipenda dal tipo di occupazione della popolazione residente. Probabilmente più le persone hanno un lavoro nel settore manageriale/professionale più sono alti i prezzi delle case.
Ma questa cosa è vera ed accade in tutti i quartieri? A questa domanda la tecnica GWR può dare una risposta. Di seguito riporto una serie di esempi riproducibili in R per rispondere a questa domanda.
Che cosa è la regressione geografica pesata — Geographically Weighted Regression (GWR)
La regressione geografica pesata, in inglese chiamata Geographically weighted regression (GWR) è uno strumento molto utile per esplorare l’eterogeneità spaziale dei dati e la relazione tra le diverse variabili.
Un tipico modello di regressione lineare su un modello è della forma:
dove
si stima attraverso la massima verosimiglianza. L’eterogeneità spaziale di un modello si ottiene con una formula del tipo:
dove le costanti 
La stima di questi parametri può fornire una valutazione della eterogeneità spaziale del dataset. In termini più semplici, stiamo esplorando se la relazione tra le variabili predittive (il tipo di occupazione nell’esempio sopra) e la variabile di risultato (il prezzo al metro quadro) sta cambiando geograficamente.
Un modo per farlo è utilizzare un approccio a finestra mobile.Per stimare il valore di 
Carico le librerie necessarie
library(spgwr)
library(ggplot2)
library(maptools)
library(rgdal)
library(GWmodel)Il problema che affronteremo
Come spiegato in precedenza in questo esercizio si lavorerà con i dati dei prezzi delle case, ottenuti dalla Nationwide Building Society (NBS) in Inghilterra – questo è un campione di case vendute nel 2001 con mutui organizzati da NBS a Londra e dintorni. I dati si trovano in un frame SpatialPolygonsDataFrame chiamato londonhp.
data(LondonHP)
head(data.frame(londonhp))|
| PURCHASE | FLOORSZ | TYPETRRD | GARAGE1 | PROF | optional |
|---|---|---|---|---|---|---|
| 0 | 157000 | 77 | 0 | 0 | 0.4786992 | TRUE |
| 1 | 113500 | 75 | 1 | 0 | 0.4786992 | TRUE |
| 2 | 81750 | 64 | 0 | 1 | 0.4786992 | TRUE |
| 3 | 150000 | 95 | 0 | 0 | 0.4786992 | TRUE |
| 4 | 190000 | 107 | 0 | 1 | 0.4786992 | TRUE |
| 5 | 159950 | 100 | 0 | 1 | 0.4773715 | TRUE |
Da questo, si può vedere che nel dataset è presente il prezzo di acquisto delle case (PURCHASE) e l’area della casa (FLOORSZ) sono registrati insieme a una serie di altri manufatti, come ad esempio se ha un garage (GARAGE1). Esistono anche variabili relative alle condizioni sociali del vicinato della proprietà, ad esempio se la proprietà è impiegata in lavori professionali o manageriali (PROF).
Qui, la variabile dipendente sarà il costo abitativo al metro quadrato per piano.
londonhp$PPSQM <- londonhp$PURCHASE / londonhp$FLOORSZLa distribuzione del prezzo al metro quadro si può analizzare visualizzando l’istogramma:
hist(londonhp$PPSQM,main="Prezzo al metro quadro (Sterline)",xlab="Costo al mq",ylab='Frequenza')
Dal grafico si osserva che la distribuzione è chiara con un piccolo numero di proprietà molto costose (in termini di costo per unità di superficie).
Esiste una relazione nei dati?
Ci si potrebbe ragionevolmente aspettare che le condizioni sociali in un’area influenzino i costi di una proprietà. Un modo semplice per indagare ciò è fare una regressione lineare tra la percentuale di occupazione professionale e gestionale (ridimensionata in modo tale che 1 implica che tutti i residenti economicamente attivi siano impiegati in lavori professionali o manageriali) rispetto al prezzo al metro quadrato:
linmod <- lm(PPSQM~PROF,data=londonhp)
# Store the regression model to use in a plot later
summary(linmod)
##
## Call:
## lm(formula = PPSQM ~ PROF, data = londonhp)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1079.6 -300.1 -50.6 214.5 3656.7
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 315.4 128.9 2.447 0.0149 *
## PROF 3446.1 294.4 11.704 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 549.3 on 314 degrees of freedom
## Multiple R-squared: 0.3038, Adjusted R-squared: 0.3015
## F-statistic: 137 on 1 and 314 DF, p-value: < 2.2e-16Ciò suggerisce che ci sia una forte correlazione tra le due variabili – e forse ciò non ci sorprende. Ciò è confermato visivamente dai grafici si seguito:
plot(linmod, which=3)
plot(PPSQM~PROF,data=londonhp,xlab='Tasso di occupazione Professionale/Manageriale',ylab='Costo al mq')
abline(linmod,col=2)
#salvo i residui nel dataframe
londonhp$residuals=residuals(linmod)
proj4string(londonhp)=CRS("+init=epsg:27700 +datum=OSGB36")
colours <- c("dark blue", "blue", "red", "dark red")
rw.colors <- colorRampPalette(colours)
#for speed we are just going to use the quick sp plot function, but you could alternatively store your residuals back in your LondonWards dataframe and plot using geom_point in ggplot2
spplot(londonhp,"residuals",cuts=quantile(londonhp$residuals),col.regions=colours,cex=0.5,main='Distribuzione dei residui')
Regressione Geografica Pesata GWR
Da questo grafico è evidente che esiste qualche modello spaziale dei residui (cioè i punti rosso e blu non sono distribuiti casualmente, ma sembrano esserci piccoli gruppi di punti rossi e blu in alcune parti di Londra). Dato che in questi residui sembra esserci qualche modello spaziale, ora eseguiremo un modello di regressione geograficamente ponderato per vedere come i coefficienti del modello potrebbero variare in tutta Londra.
Innanzitutto calibreremo la larghezza di banda del kernel che verrà utilizzata per acquisire i punti per ciascuna regressione (ciò potrebbe richiedere un po ’di tempo) e quindi eseguire il modello:
bwG <- gwr.sel(PPSQM~PROF,data=londonhp, gweight = gwr.Gauss, verbose = FALSE)
gwrG <- gwr(PPSQM~PROF,data=londonhp, bandwidth = bwG, gweight = gwr.Gauss, hatmatrix = TRUE)
gwrG
## Call:
## gwr(formula = PPSQM ~ PROF, data = londonhp, bandwidth = bwG,
## gweight = gwr.Gauss, hatmatrix = TRUE)
## Kernel function: gwr.Gauss
## Fixed bandwidth: 1592.69
## Summary of GWR coefficient estimates at data points:
## Min. 1st Qu. Median 3rd Qu. Max. Global
## X.Intercept. -5427.41 630.96 1070.89 1829.18 26892.85 315.36
## PROF -54667.56 -106.57 1151.68 2593.03 21993.88 3446.12
## Number of data points: 316
## Effective number of parameters (residual: 2traceS - traceS'S): 82.56297
## Effective degrees of freedom (residual: 2traceS - traceS'S): 233.437
## Sigma (residual: 2traceS - traceS'S): 343.9272
## Effective number of parameters (model: traceS): 69.17997
## Effective degrees of freedom (model: traceS): 246.82
## Sigma (model: traceS): 334.4731
## Sigma (ML): 295.6023
## AICc (GWR p. 61, eq 2.33; p. 96, eq. 4.21): 4673.395
## AIC (GWR p. 96, eq. 4.22): 4561.407
## Residual sum of squares: 27612316
## Quasi-global R2: 0.7970772L’output del modello GWR rivela come i coefficienti variano tra le 316 proprietò analizzate di Londra. Vedrai come i coefficienti globali sono esattamente gli stessi dei coefficienti nel precedente modello lineare. In questo particolare modello, se prendiamo la percentuale di occupazione, possiamo vedere che per metà dei casi analizzati (l’intervallo tra il primo quartile 1st Qu e il 3rd Qu) un aumento di un punto percentuale dell’occupazione causa un aumento dei prezzi al metro quadro tra -10 e 295 con una mediana di 115.
Analisi dei risultati delle vendite a Londra
Si estraggono i risultati dei residui
data(LondonBorough)
#assegno il sistema di riferimento
proj4string(londonborough)=CRS("+init=epsg:27700 +datum=OSGB36")
#prendo i risultati del modello
results<-as.data.frame(gwrG$SDF)
head(results)
## sum.w X.Intercept. PROF X.Intercept._se PROF_se gwr.e
## 1 5.097600 -2873.7522 9420.155 4021.6569 8579.010 403.29264
## 2 5.536862 -1872.9458 7312.165 2844.3804 6108.554 -114.04835
## 3 4.889233 -171.8019 3700.074 1131.8928 2577.136 -322.07707
## 4 4.885489 131.2473 3049.958 902.0210 2096.322 -12.31243
## 5 6.062372 -264.0691 3893.688 1100.3421 2476.619 175.86463
## 6 5.710936 606.2565 2013.864 787.7687 1807.535 31.88232
## pred pred.se localR2 X.Intercept._se_EDF PROF_se_EDF pred.se.1
## 1 1635.668 128.0724 0.08845230 4135.3316 8821.501 131.6925
## 2 1627.382 121.6083 0.10217072 2924.7786 6281.216 125.0456
## 3 1599.421 133.9493 0.08995998 1163.8864 2649.980 137.7355
## 4 1591.260 131.8729 0.09311107 927.5172 2155.576 135.6004
## 5 1599.836 116.8833 0.12058231 1131.4440 2546.622 120.1871
## 6 1567.618 122.1208 0.12886376 810.0354 1858.626 125.5726
## coords.x1 coords.x2
## 1 533200 159400
## 2 533300 159700
## 3 532000 159800
## 4 531900 160100
## 5 532800 160300
## 6 535700 161700
#estraggo i coefficienti dei residui e li inserisco del dataframe originale
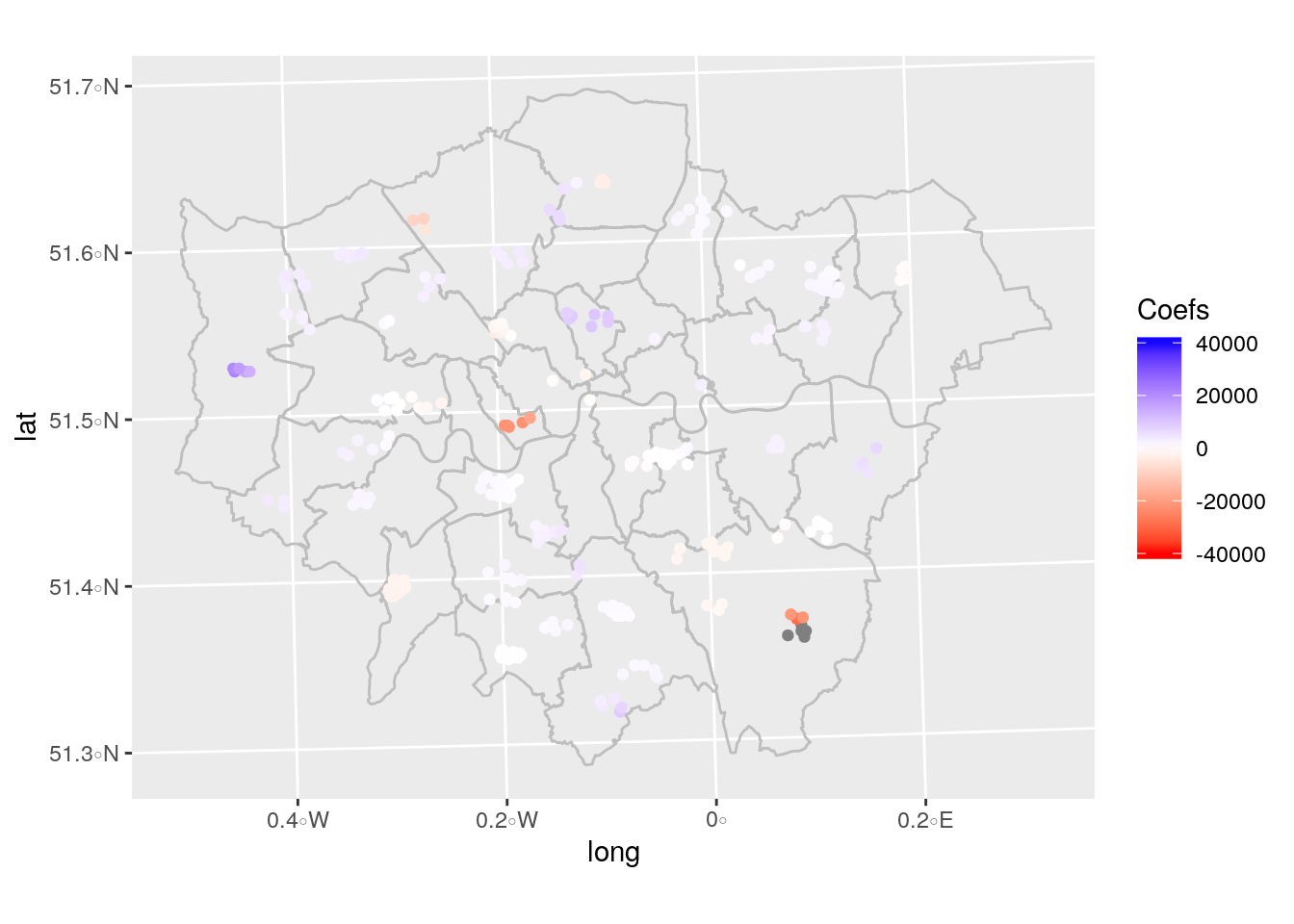
londonhp$coefPROF<-results$PROFSi passa ai grafici dei residui
library(ggspatial)
LondonBoroughline <- fortify(londonborough, region="NAME")
pp1=ggplot()+geom_polygon(data=LondonBoroughline,aes(long, lat, group=id), colour="grey",fill = NA)+layer_spatial(londonhp,aes(col=coefPROF))
pp1+scale_colour_gradient2(low = "red", mid = "white", high = "blue", midpoint = 200, space = "rgb", na.value = "grey50", guide = "colourbar", guide_legend(title="Coefs"),limits=c(-40000,40000))
## Warning: Non Lab interpolation is deprecated
Il grafico suggerisce che la correlazione è positiva nel centro di nord di Londra ma negative in altre aree. Ovvero non sempre al crescere del tasso di occupazione cresce anche il prezzo al metro quadro delle abitazioni.